Verwandle kalte Besucher in treue Kunden mit einem einfachen System
Verlassen Sie sich nicht mehr nur auf Empfehlungen & Kaltakquise. Wir bauen für B2B Unternehmen ein System auf, das Verkehr generiert, Vertrauen aufbaut und diesen automatisch konvertiert.
4.8 Sterne nach 3.741 Downloads

Einige unserer Kunden






Die 4 größten Probleme von B2B Unternehmen
1. Sie erhalten keine Besucher/Verkehr
Wenn niemand Sie kennt, wird keiner bei Ihnen kaufen. Die Generierung von zielgerichtetem Verkehr ist der erste Schritt.

2. Mangelndes Vertrauen führen zu hohen Lead Kosten
Auch wenn man Sie kennt, müssen Sie ohne Vertrauen viel Geld für qualifizierte Leads ausgeben und wachsen nicht.

3. Die Verwandlung in Termine & Kunden ist gering.
Die Handlunsaufforderung “Jetzt Termin vereinbaren” ist kein effektives System zur Lead Erfassung und Pflege.

4. Fast alle Kunden kommen durch Empfehlungen.
Empfehlungen bestätigen die Qualität ihrer Arbeit. Doch ausschließlich darauf zu setzen, macht Sie von anderen abhängig.

Das B2B Lead System von Marketing Hilfe
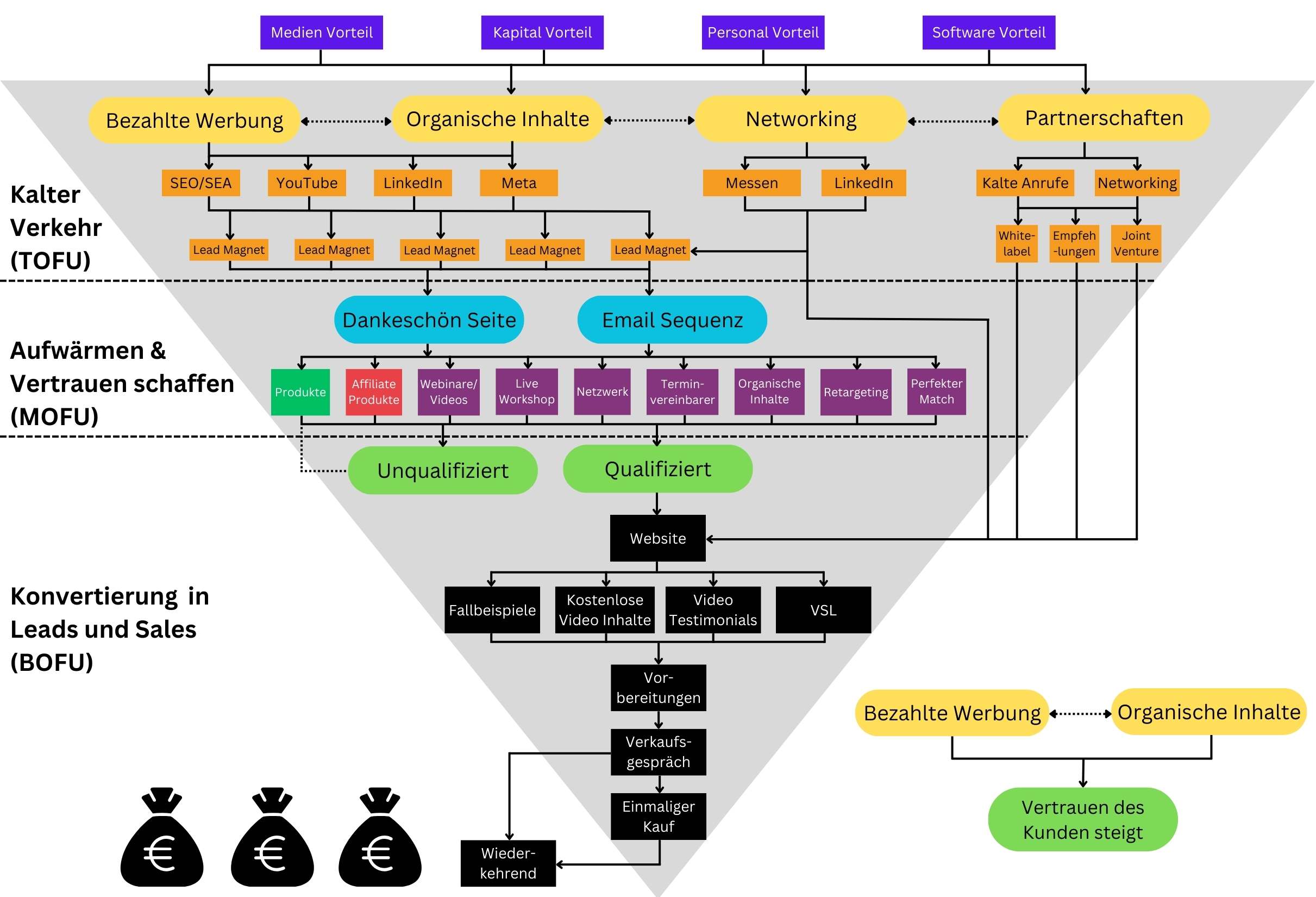
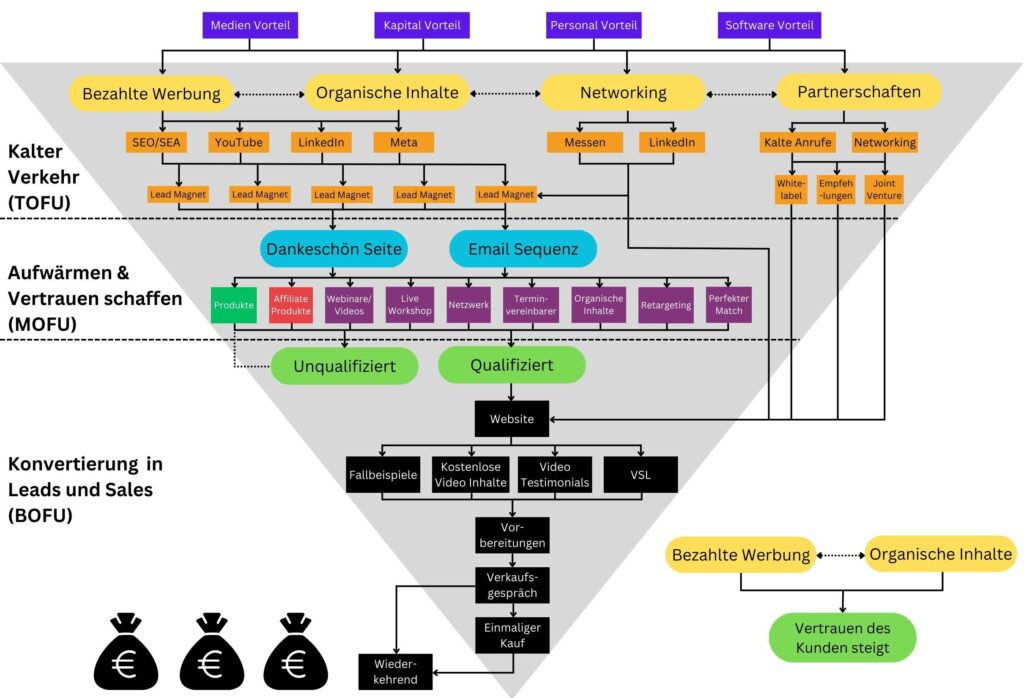
Unser schlanker Prozess stellt Ihnen das komplette Werkzeug zur Verfügung, um die 4 Hauptprobleme zuverlässig zu lösen. Wir unterstützen Sie beim Aufbau, der Implementierung und dem Testen.
4.8 Sterne nach 3.741 Downloads
Im ersten Schritt generieren wir Verkehr und erstellen relevante Lead Magneten, um die Daten von Interessenten zu erhalten.
Verkehr/Leads.
Anschließend bauen wir durch den Newsletter, Workshops, Blog Artikel und Video Inhalte vertrauen auf.
Vertrauen.
Die Konversation wird durch Retargeting Werbung, Termin Vereinbarer und Verweise im Newsletter garantiert.
Konversation.
Wir werden alle Aktivitäten tracken und ihre Präsenz anhand der Daten kontinuierlich verbessern.
Analyse.
Hi! Ich bin Online Marketing Experte René Gerhardt
*auf dem Bild rechts 😉
Nach mehr als 10 Jahren des Erstellens und Testens von Marketingstrategien für Unternehmen habe ich gelernt, was funktioniert (und was nicht).
Viele setzten entweder, ihr Vertrauen in bezahlte Medien ohne organisches Wachstum oder haben mit gesättigten Märkten zu kämpfen.
Sich auf die 20% des Inhalts, Werbung und sozialen Strategien zu konzentrieren, die die größten Erfolge für Ihr Unternehmen bringen, ist das Geheimnis, um Ihr Geschäft schnell zu skalieren – ohne Burnout.
Wenn Sie bereit sind, mehr zu erreichen, indem Sie deutlich weniger tun, dann kontaktieren Sie uns gerne!
Lassen Sie uns dies in die Realität umsetzen.
Liebe Unternehmer,
Sie wurden mit Marketing-“Geheimnissen” und -“Kniffen” bombardiert, die Ihnen das Blaue vom Himmel versprechen, aber maximal eine Landkarte geliefert haben.
In dieser digitalen Wildnis, in der Sie umherirren, ist es übersät mit überteuerten Consultants, die veraltete Strategien verkaufen.
Sie führen Sie im Kreis herum, nicht zum Schatz.
Es ist Zeit für eine Realitätsprüfung.
Was gestern funktionierte, muss heute nicht unbedingt wirksam sein.
Sie brauchen mehr als nur Taktiken und schlaue Worte.
Sie brauchen eine umsetzbare Strategie, die durch den Lärm schneidet, einen Kompass, der wirklich nach Norden zeigt.
Tag für Tag werfen Sie alles an die Wand – SEO, soziale Medien, Werbung – in der Hoffnung, dass etwas hängen bleibt.
Hier ist ihre Wendung:
Stellen Sie sich vor, Sie entdecken einen geheimen Erzählfaden, der sich durch jede erfolgreiche Kampagne zieht.
Lassen Sie uns durch den Lärm schneiden und unsere Strategie enthüllen: Storytelling, das verkauft!
Das Herzstück unseres Marketing Arsenals. Es ist mehr als nur eine Taktik.
Es ist eine Kunstform.
Ein tolles Produkt zu haben, reicht nicht aus.
Sie müssen wissen, wie Sie darüber sprechen, um es in den Köpfen und Herzen Ihres Publikums lebendig zu machen.
Heutzutage kann jedes Kind, Besucher bei Meta kaufen..
Es ist so einfach!
Meine Vermutung wäre, die Ergebnisse sind enttäuschend.

Eine gut erzählte Geschichte kann bis zu 22-mal einprägsamer sein als bloße Fakten.
Es ist an der Zeit, sich zu fragen, welche Geschichte Ihre Marke erzählt.
Welche Emotionen ruft sie hervor?
Denken Sie daran, die Menschen vergessen vielleicht die Einzelheiten dessen, was Sie sagen, aber sie werden sich immer daran erinnern, wie Sie sie sich fühlten.
Das ist die Kraft des Storytellings im Geschäftsbereich – es treibt Käufe weit effektiver an als Logik.
Beim Entwerfen Ihrer Botschaft, denken Sie darüber nach, was Ihre Zielgruppe wirklich von Ihnen braucht (zusätzlich zu einem Produkt oder einer Dienstleistung).
Nehmen Sie zum Beispiel Apple:
Sie verkaufen Technologie, aber von Anfang an musste sich ihr Publikum so fühlen, als wäre es in Ordnung (und sogar erwünscht), mutig, kühn und anders als die Masse zu denken.
Teslas Kunden müssen das Gefühl haben, dass es sich lohnt, die Umwelt und nachhaltige Energie zu unterstützen.

Damit ihre Marke abhebt, wie eine SpaceX Rakete müssen sie so viel mehr als ein Produkt oder Dienstleistung werden..
Und hier kommt das Storytelling ins Spiel.
Überlegen Sie, welche Emotionen, Werte und Ideen Sie Ihrer Zielgruppe bieten können.
Sobald Ihr Publikum Sie kennt, Ihnen vertraut und Sie mag, werden sie wahrscheinlicher bei Ihnen kaufen.
Im besten Fall haben Sie Beziehungen zu Menschen aufgebaut, die noch Jahre später Fürsprecher sein werden.
Bei Mhilfe sind wir mehr als nur eine Online Marketing Agentur.
Wir sind die Hüter Ihrer Markenerzählung.
Wir gehen über das bloße Generieren von Besuchern und das Erstellen beeindruckender Websites hinaus..
Und tauchen tief ein, um sicherzustellen, dass Ihre Geschichte in jeden Aspekt Ihres Marketings eindrucksvoll eingewoben wird..
Von Anzeigen über Landing Pages, SEO bis hin zu Social Media Ads.
Wir sind hier, um Ihre Marke unvergesslich zu machen.
Betreiben Sie nicht nur Marketing..
Starten Sie eine Bewegung mit Ihrer Geschichte.
Leistungen
B2B SEO Agentur
Dies ist wahrscheinlich die rentabelste Art Besucher zu erhalten, welche auf unserem Planeten existiert. Sie können über Jahre kostenlos Personen auf Ihre Website leiten, die gezielt nach Ihrem Produkt oder Dienstleistung suchen.
Social Media Marketing
Mit mehr als 72,6 Millionen Menschen, die allein in Deutschland in sozialen Medien aktiv sind, ist der beste Ort, um die Aufmerksamkeit der Menschen zu erregen, die sozialen Medien. Mit dem richtigen Targeting und Inhalten erreichen Sie ihre Kunden effektiv.
SEA Online Marketing (Google Ads)
Stellen Sie sich vor, es existiert eine Maschine, die jedes Mal, wenn Sie 1 Euro hineinlegen, 2 Euro ausspuckt. Wie viel würden Sie investieren? Genau das könnte Google Ads für Ihr Unternehmen bewirken, wenn es effektiv genutzt wird.
Online Reputation Management
Kunden sind heutzutage äußerst skeptisch. Vor einem Kauf suchen sie oft nach Ihrer Marke auf Google. Erscheinen negative Suchergebnisse für Ihre Marke, helfen wir Ihnen, diese zu korrigieren.
Sind wir die richtige Online Marketing Agentur für Sie?
Wir sind eine strategische Online Marketing Agentur, die darauf spezialisiert ist, systematisch kalte Besucher in treue Kunden zu verwandeln.
Natürlich verstehen wir, dass die Wahl der richtigen Agentur für Ihr Unternehmen keine leichte Entscheidung, daher erfahren Sie hier mehr über uns.